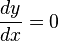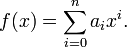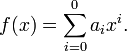Funciones pares
Se dice que una función f es par cuando para cualquier x en el dominio de f se tiene que f(-x)=f(x).
Funciones impares
Se dice que una función es par si f(x) = f(-x), en el caso de que f(x) = -f(-x) se dice que la función es impar.
Ejemplos 1:
La función y(x)=x es impar ya que:
f(-x) = -x
pero como f(x) = x entonces:
f(-x) = - f(x).

Otra función impar es y = 1/x
Cuando f(x) = -f(-x)

Ejemplo 3:
La función f(x)=x2 es par ya que f(-x) = (-x)2 =x2

Función estrictamente creciente en un intervalo
Una función  es estrictamente creciente en un intervalo
es estrictamente creciente en un intervalo  , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,  y
y  , se cumple que:
, se cumple que:
 es estrictamente creciente en un intervalo
es estrictamente creciente en un intervalo  , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,  y
y  , se cumple que:
, se cumple que:
Cuando en la gráfica de una función estrictamente creciente nos movemos hacia la derecha tambien nos movemos hacia arriba:

Una función  es estrictamente creciente en el punto de abcisa
es estrictamente creciente en el punto de abcisa  si existe algun número positivo
si existe algun número positivo  tal que
tal que  es estrictamente creciente en el intervalo
es estrictamente creciente en el intervalo  .
.
 es estrictamente creciente en el punto de abcisa
es estrictamente creciente en el punto de abcisa  si existe algun número positivo
si existe algun número positivo  tal que
tal que  es estrictamente creciente en el intervalo
es estrictamente creciente en el intervalo  .
.De esta esta definición se deduce que si  es derivable en
es derivable en  y
y  es estrictamente creciente en el punto de abcisa
es estrictamente creciente en el punto de abcisa  , entonces
, entonces  .
.
 es derivable en
es derivable en  y
y  es estrictamente creciente en el punto de abcisa
es estrictamente creciente en el punto de abcisa  , entonces
, entonces  .
.Función creciente en un intervalo
Una función  es creciente en un intervalo
es creciente en un intervalo  , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,  y
y  , se cumple que:
, se cumple que:
 es creciente en un intervalo
es creciente en un intervalo  , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,  y
y  , se cumple que:
, se cumple que:
Función estrictamente decreciente en un intervalo
Una función  es estrictamente decreciente en un intervalo
es estrictamente decreciente en un intervalo  , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,  y
y  , se cumple que:
, se cumple que:
 es estrictamente decreciente en un intervalo
es estrictamente decreciente en un intervalo  , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,  y
y  , se cumple que:
, se cumple que:
Cuando en la gráfica de una función estrictamente decreciente nos movemos hacia la derecha tambien nos movemos hacia abajo:

Una función  es estrictamente decreciente en el punto de abcisa
es estrictamente decreciente en el punto de abcisa  si existe algun número positivo
si existe algun número positivo  tal que
tal que  es estrictamente decreciente en el intervalo
es estrictamente decreciente en el intervalo  .
.
 es estrictamente decreciente en el punto de abcisa
es estrictamente decreciente en el punto de abcisa  si existe algun número positivo
si existe algun número positivo  tal que
tal que  es estrictamente decreciente en el intervalo
es estrictamente decreciente en el intervalo  .
.De esta esta definición se deduce que si  es derivable en
es derivable en  y
y  es estrictamente decreciente en el punto de abcisa
es estrictamente decreciente en el punto de abcisa  , entonces
, entonces  .
.
 es derivable en
es derivable en  y
y  es estrictamente decreciente en el punto de abcisa
es estrictamente decreciente en el punto de abcisa  , entonces
, entonces  .
.Función decreciente en un intervalo
Una función  es decreciente en un intervalo
es decreciente en un intervalo  , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,  y
y  , se cumple que:
, se cumple que:
 es decreciente en un intervalo
es decreciente en un intervalo  , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,  y
y  , se cumple que:
, se cumple que:
Función constante
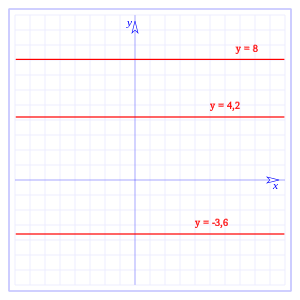
En matemática se llama función constante a aquella función matemática que toma el mismo valor para cualquier valor de la variable. Se la representa de la forma:
donde a es la constante.
Funciones reales de una variable real
Como se puede ver es una recta horizontal en el plano xy, en la gráfica la hemos representado en el plano, pero, como se puede ver la función no depende de x, si hacemos:
tenemos:
donde a tiene un valor constante, en la gráfica tenemos representadas:
Como la variable dependiente y no depende de x tenemos que:
la variación de y respecto a x es cero
]La función constante como un polinomio en x
Si un polinomio general, que tiene la forma:
una función constante cumple esta expresión con n= 0, es un polinomio de grado 0.
que es lo mismo que:
que corresponde al termino independiente del polinomio.